Time and Distance Formula
To solve the question related to time, distance and speed/
velocity each and every candidates will have to learn all the formulas related
to the questions. In this article ejobhub is going to release all the details
having all the possible Shortcuts, Methods & Tricks Online for those
candidates/ students who are looking to reach in the comfort zone at the time
of solving the questions connected with Time and Distance problems. In
quantitative aptitude section, ambitious participants spend more time due to not
friendly with formulas, shortcuts and short tricks to solve problems. If you
know the shortcuts, methods and short tricks then very less time is required to
get the right answer of such questions.
Competitive exams give very tough competition because of
fewer vacancies and more candidates. To get success in the exam applicants need
to show accuracy and speed. To have both of them aspirants can become winner in
the test. Formula of distance, speed and time is correlated with each other
(SPEED = DISTANCE / TIME), so friends learn them. Candidates are suggested to prepare
with the help of sample papers and previous year question papers for the
upcoming exams for any post in which exam will be scheduled with quantitative
aptitude section (Maths). More details in favour of Time and Distance Formula
are given below. Have a close look-
Time and Distance Formulas and how to convert Them
Basics:
Know all the combinations of Time and Distance Formula-
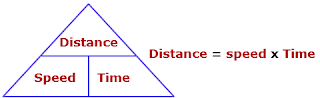
1. DISTANCE = SPEEDX TIME
2. SPEED = DISTANCE / TIME
3. TIME = DISTANCE / SPEED
Conversion of Unit:
Generally we measure speed in km/h but sometime it is said that find speed in
meter per second then we should remind this formula-
Convert kilometers per hour (km/hr) to meters per second
(m/s): Check below-
x
km/hr = x X 5/18 m/s
Convert meters per second (m/s) to kilometers per hour
(km/hr): Check below-
x m/s= x X 18/5 km/hr
Average Speed:If
an object covers a certain distance at x kmph and an equal distance at y kmph,
the average speed of the whole journey-
Speedavg = Total distance covered by object/
total time taken to cover the distance
=2xy/x+y kmph
Relation between Distance,
Speed and Time: Speed and time are inversely proportional (when
distance is constant). That is-
⟹speed∝1/time (when distance is constant)
If the ratio of the speeds of A and B is a:b, then, the
ratio of the time taken by them to cover the same distance is
1/a:1/b=b:a
Suppose two objects A and B start at the same time in
opposite directions from P and Q respectively. After passing each other, A
reaches Q in a seconds and B reaches P in b seconds. Then,
Speed of A: Speed of B =√b:√a
An object covered a certain distance at a speed of v kmph.
If it had moved v1 kmph faster, it would have taken t1 hours less. If it had
moved v2 kmph slower, it would have taken t2 hours more. Then,
Speed (V) = [v1v2(t1 + t2)
/ v1t2 – v2t1] kmph
Distance (x) = [vt1(1 + v/v1)] km
Special case:
If t1 = t2,
v = 2v1v2/( v1 – v2)
kmph
Relative Speed:
If two objects are moving in the same direction at v1 m/s and v2
m/s respectively
where v1>v2, then their relative
speed = (v1−v2) m/s
Let us suppose that two objects A and B separated by a
distance of d meter. Suppose A and B start moving in the same direction at the
same time such that A moves towards B at a speed of a meter/second and B moves
away from A at a speed of b meter/second where a>b. Then,
Relative speed = (a−b) meter/second
Time needed for A to meet B =d/(a−b) seconds
If two objects are moving in opposite directions at v1
m/s and v2 m/s respectively, then their relative
speed =
(v1+v2) m/s
Consider two objects A and B separated by a distance of d
meter. Suppose A and B start moving towards each other at the same time at a
meter/second and b meter/second respectively. Then,
Relative speed = (a+b) meter/second
Time needed for A and B to meet each other =d/(a+b) seconds
Reminder:
Dear candidates now you are very close to success in the section of quantitative
aptitude using above shortcuts of formulas. All the best!!
Take a Look on Below Table



0 comments:
Post a Comment